 Even though most of people work tirelessly for the paycheck day in and day out, it sometimes doesn’t come as much as they need. Unfortunately, many payments are uncontrolled and can put you in financial trouble from time to time. There is an excellent short-term answer to the urgent payments in a form of San Diego payday loans available for the citizens of this beautiful city in California. Typically, consumers have to face lengthy loan procedures while borrowing money in a traditional way, however, with paycheck loans offered by our company you can set yourself free from the bothering processes. Our service is meant for those people who need cash desperately within a few hours to meet unforeseen expenses, therefore, our professional team works fast providing money the same day.
Even though most of people work tirelessly for the paycheck day in and day out, it sometimes doesn’t come as much as they need. Unfortunately, many payments are uncontrolled and can put you in financial trouble from time to time. There is an excellent short-term answer to the urgent payments in a form of San Diego payday loans available for the citizens of this beautiful city in California. Typically, consumers have to face lengthy loan procedures while borrowing money in a traditional way, however, with paycheck loans offered by our company you can set yourself free from the bothering processes. Our service is meant for those people who need cash desperately within a few hours to meet unforeseen expenses, therefore, our professional team works fast providing money the same day.
Online Payday Loans In San Diego Are Approved Instantly
Sometimes salaried people don’t get their money on time and have to pay expensive penalties on current bills. Instant payday loans in San Diego don’t contain lengthy and time consuming processes of faxing and personal visit, thus, direct lenders make instant approval and the borrowers applying for the service are able to receive the requested cash in 1 hour. Credit card payments, medical expenses, costs of small home improvement, car repair, insurance premium – all these bills can occur in the middle of the month creating various difficulties for working people. Still, they can be easily solved with online loans performed by our company. In order to borrow the necessary amount of money, take the help of the Internet and apply for faxless loans online through our website.
San Diego Paycheck Loans Provided With No Faxing
Conventional banks don’t typically lend money without having collateral as well as traditional lending stores request to visit their locations and stay in line. This usually takes a lot of time and sometimes even days to get financed. Isn’t it much better to take out San Diego CA payday loan online without leaving home? All you need is to go online and complete our simple application form suggested on the site. The requested funds will be deposited directly to your bank account even if you have bad credit score. Since there is no credit check or faxing any borrower can enjoy the advantages of our speedy service. There is no sense to visit the lender in person when you can use an affordable alternative form of lending performed on the Internet.
Get San Diego Payday Advance Loans With Bad Credit Score
We understand that the contemporary life brings a lot of stresses which weigh on you, therefore, we would like to help you solve some of your problems, at least those concerning unexpected expenses. You can get the needed amount of money in one hour simply by submitting our easy application. All we require is your basic financial and personal information that will allow lenders to approve your application and to supply you with cash instantly. Apply for our no credit check payday loans in San Diego when urgent expenses knock the door. Pass through the simplest application procedure you have ever faced and get the money you need the same day!
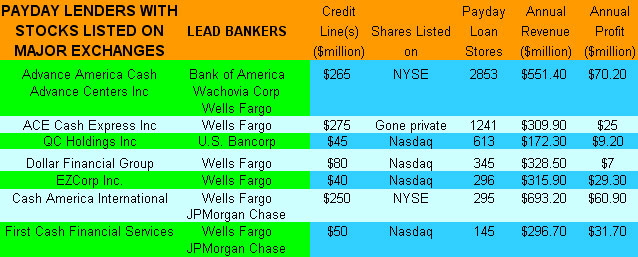 In their defense, banks, including B of A have begun to impose stricter rules for compliance.
In their defense, banks, including B of A have begun to impose stricter rules for compliance. Believe it or not, as we reported in a previous article, 65% of Americans do not have a personal budget. A budget is an essential tool to get a handle on where your money is being spent.
Believe it or not, as we reported in a previous article, 65% of Americans do not have a personal budget. A budget is an essential tool to get a handle on where your money is being spent. This Winter on December 21, the
This Winter on December 21, the  If you live in Texas, you will be interested in recent legislation submitted by Representative Vicki Truitt, R-Keller, and chairwoman of the House Pension, Investments and Financial Services Committee, who this week introduced a package of legislation reported by the Star-Telegram. The legislation would require lenders to register with the Consumer Credit Commissioner, which could deny an application based on criminal record, as well as require lenders to file annual reports. Her main goal is to punish and eliminate unethical lenders.
If you live in Texas, you will be interested in recent legislation submitted by Representative Vicki Truitt, R-Keller, and chairwoman of the House Pension, Investments and Financial Services Committee, who this week introduced a package of legislation reported by the Star-Telegram. The legislation would require lenders to register with the Consumer Credit Commissioner, which could deny an application based on criminal record, as well as require lenders to file annual reports. Her main goal is to punish and eliminate unethical lenders.